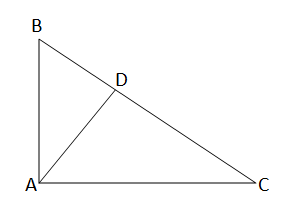
---

\(\triangle\)ABC এর AD\(\bot\)BC এবং AD\(^2\)=BD.DC
তাহলে প্রমান করতে হবে যে, \(\angle\)BAC =90\(^o\)

প্রমান : ABD একটি সমকোণী ত্রিভূজ যার, \(\angle\)ADB=90\(^o\)
\(\therefore \) AB\(^2\)=AD\(^2\)+BD\(^2\) \(-----(i)\)[ পিথাগোরাসের উপপাদ্য থেকে পাই ]

আবার, ADC সমকোণী ত্রিভূজের \(\angle\)ADC=90\(^o\)
\(\therefore \) AC\(^2\)=AD\(^2\)+CD\(^2\) \(-----(ii)\)[ পিথাগোরাসের উপপাদ্য থেকে পাই ]

\((i)\) ও \((ii)\) যোগ করে পাই,
AB\(^2\)+AC\(^2\)=AD\(^2\)+BD\(^2\) +AD\(^2\)+CD\(^2\)
=BD\(^2\) +CD\(^2\)+2AD\(^2\)
=BD\(^2\) +CD\(^2\)+2BD.CD [\(\because \) AD\(^2\)=BD.CD]
=(BD+CD)\(^2\) =BC\(^2\)

\(\therefore\) AB\(^2\)+AC\(^2\)=BC\(^2\)

\(\therefore\) পিথাগোরাসের বিপরীত উপপাদ্য থেকে পাই, ABC সমকোণী ত্রিভূজের \(\angle\)BAC একটি সমকোণ (প্রমাণিত)