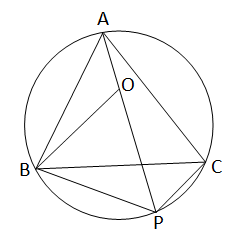
---

ধরি \(\triangle\)ABC একটি বৃত্তস্থ সমবাহু ত্রিভূজ। BC চাপের ওপর P যেকোনো একটি বিন্দু ।
প্রমান করতে হবে যে, AP=BP+CP

অঙ্কন : AP থেকে PC এর সমান করে AO কেটে নেওয়া হল । BO, BP ও CP যুক্ত করা হল ।

প্রমান : \(\triangle\)ABO ও \(\triangle\)BPC এর
AO=PC (অঙ্কনানুসারে)
AB=BC (\(\because\) \(\triangle\)ABC সমবাহু ত্রিভূজ)
এবং \(\angle\)BAO=\(\angle\)BCP (একই চাপের ওপর পরিধিস্থ কোণ)
\(\therefore \triangle\)ABO \( \cong \triangle\)BPC
\(\therefore \) BO=BP
\(\therefore \angle\)BOP=\(\angle\)BPO=\(\angle\)ACB (একই চাপের উপর পরিধিস্থ কোণ)=60\(^o\)
\(\therefore \angle\)OBP=60\(^o\)=\(\angle\)BOP
\(\therefore\) BP=PO
\(\therefore\) AP=PO+AO=BP+PC