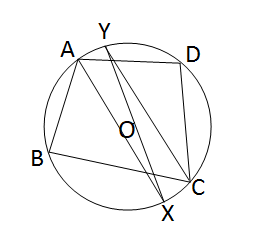
---

প্রদত্ত : ABCD বৃত্তস্থ চতুর্ভূজের \(\angle\)DAB ও \(\angle\)BCD এর সমদ্বিখন্ডকদ্বয় বৃত্তকে X ও Y বিন্দুতে ছেদ করে ।

প্রমান করতে হবে যে : XY বৃত্তের ব্যাস ।

অঙ্কন : A, Y বিন্দুদ্বয় যোগ করা হল ।

প্রমান : \(\angle\)YAB ও \(\angle\)YCB বৃত্তের উপচাপ YB এর দ্বারা গঠিত একই বৃত্তাংশস্থ কোণ ।
\(\therefore \angle\)YAB=\(\angle\)YCB=\(\cfrac{1}{2}\angle\)BCD\(-----(i)\) [\(\because\) CY, \(\angle\)BCD এর সমদ্বিখন্ডক]

আবার, \(\angle\)XAY=\(\angle\)XAB+\(\angle\)YAB
\(=\cfrac{1}{2}\)(\(\angle\)BAD+\(\cfrac{1}{2}\)\(\angle\)BCD [\((i)\) থেকে পেলাম] [\(\because\) AX, \(\angle\)DAB -এর সমদ্বিখন্ডক ]
\(=\cfrac{1}{2}\)(\(\angle\)BAD+\(\angle\)BCD)
\(=\cfrac{1}{2}\times\)180° [\(\because\) ABCD বৃত্তস্থ চতুর্ভূজ]
\(=\)90°

\(\therefore \angle\)XAY একটি অর্ধবৃত্তস্থ কোণ ।
\(\therefore\) XY বৃত্তের ব্যাস ।