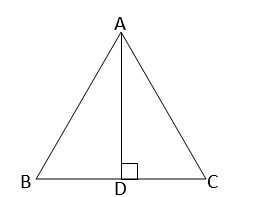
---

ধরি, \(∆ABC\) সমবাহু ত্রিভূজের \(AD,BC\) বাহুর ওপর লম্ব।
প্রমান করতে হবে যে, \(AB^2 + BC^2 + CA^2= 4AD^2\)
\(∵ ∆ABD\) একটি সমকোণী ত্রিভূজ,তাই পিথাগোরাসের সূত্র থেকে পাই
\(AB^2=AD^2+BD^2\)
বা, \(AB^2=AD^2+\left(\cfrac{1}{2} BC\right)^2=AD^2+\cfrac{1}{4} BC^2\)
\(=\cfrac{4AD^2+BC^2}{4}=\cfrac{4AD^2+AB^2}{4} \) \([∵AB=BC]\)
বা, \(4AB^2=4AD^2+AB^2\)
বা, \(3AB^2=4AD^2 \)
বা, \(AB^2+AB^2+AB^2=4AD^2 \)
বা, \(AB^2+BC^2+CA^2=4AD^2 \) (প্রমানিত) \([∵AB=BC=CA]\)