প্রমাণ করো যে বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক। Madhyamik 2022 , 2023
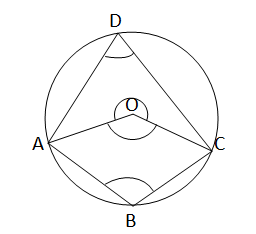
প্রদত্ত:O কেন্দ্রীয় বৃত্তে ABCD একটি বৃত্তস্থ চতুর্ভূজ।
প্রমান করতে হবে যে:∠ABC+∠ADC=2 সমকোণ এবং ∠BAD+∠BCD=2 সমকোণ
অঙ্কন:A,O এবং C,O যোগ করলাম।
প্রমান:ADC বৃত্তচাপ দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠AOC এবং বৃত্তস্থ কোণ ∠ABC
∴প্রবৃদ্ধ ∠AOC=2∠ABC
∴∠ ABC= \(\frac{1}{2}\) প্রবৃদ্ধ ∠AOC----(i)
আবার ABC বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠AOC এবং বৃত্তস্থ কোণ ∠ADC
∴∠AOC=2∠ADC
∴∠ADC=\(\frac{1}{2}\) AOC----(ii)
∴(i)এবং (ii)হইতে পাই,
∠ABC+∠ADC=\(\frac{1}{2}\) প্রবৃদ্ধ∠AOC+\(\frac{1}{2}\) ∠AOC
=\(\frac{1}{2}\) (প্রবৃদ্ধ ∠AOC+∠AOC)
=\(\frac{1}{2}\)×4 সমকোণ
=2 সমকোণ
অনুরূপে B,O এবং D,O যোগ করে প্রমান করতে পারি যে,∠BAD+∠BCD=2 সমকোণ [প্রমাণিত]