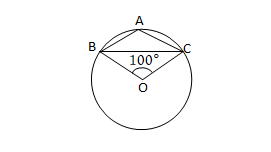
---

সমদ্বিবাহু ∆ABC এর AB=AC এবং পরিকেন্দ্র O,BC বাহুর যেদিকে A বিন্দু রয়েছে তার বিপরীত দিকে O বিন্দু রয়েছে।

BC চাপের ওপর \(\angle\)BAC এবং প্রবৃদ্ধ \(\angle\)BOC অবস্থিত ।

∴2\(\angle\)BAC=প্রবৃদ্ধ\(\angle\)BOC
বা,2\(\angle\)BAC=(360°-100°)=260°
অর্থাৎ,\(\angle\)BAC=130°

∆ABC এর,AB=AC
∴\(\angle\)ABC=\(\angle\)ACB=\(\frac{1}{2}\) (180°-\(\angle\)BAC) =\(\frac{1}{2}\) (180°-130°)=\(\frac{50°}{2}\)=25°

আবার ∆BOC এর,
OB=OC [উভয়েই বৃত্তের ব্যাসার্ধ]
∴\(\angle\)OBC=\(\angle\)OCB=\(\frac{1}{2}\)(180°-\(\angle\)BOC) =\(\frac{1}{2}\)(180°-100°)=\(\frac{80°}{2}\)=40°

∴\(\angle\)ABO=\(\angle\)ABC+\(\angle\)OBC=25°+40° =65°

∴\(\angle\)ABC=25° এবং \(\angle\)ABO=65° (Answer)