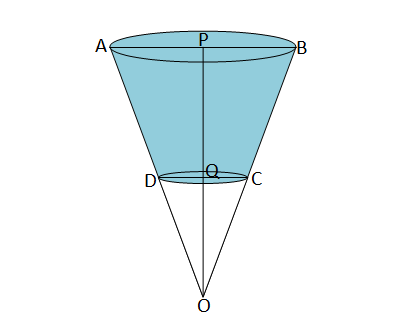
---

ধরি, PQ=24 সেমি উচ্চতাবিশিষ্ট একটি বালতি ABCD এর দুই প্রান্তের ব্যাসার্ধ যথাক্রমে AP=15 সেমি এবং DQ=5 সেমি।

এখন বালতিটিকে একই ঢাল বরাবর কাল্পনিকভাবে বাড়ালে বালতিটি একটি ABO শঙ্কুর আকৃতি নেয় । এখন শঙ্কু ABO এবং শঙ্কু DCO এর আয়তনের অন্তরই হবে বালতিটির আয়তন ।

ধরি, OQ=\(x\) সেমি

সুতরাং সদৃশকোণী ত্রিভূজ \(\triangle\)APO এবং \(\triangle\)DQO থেকে পাই,
\(\cfrac{AP}{OP}=\cfrac{DQ}{OQ}\)
বা, \(\cfrac{15}{PQ+OQ}=\cfrac{5}{x}\)
বা, \(\cfrac{15}{24+x}=\cfrac{5}{x}\)
বা, \(15x=120+5x\)
বা, \(15x-5x=120\)
বা, \(x=\cfrac{120}{10}=12\)

\(\therefore\) OP=(24+12) সেমি =36 সেমি ।

\(\therefore\) বালতিটির আয়তন = ABO শঙ্কুর আয়তন - DCO শঙ্কুর আয়তন
\(=[\cfrac{1}{3}\pi 15^2\times 36 -\cfrac{1}{3}\pi 5^2\times 12]\) ঘন সেমি
\(=\cfrac{1}{3}\pi[225\times 36 -25\times 12]\) ঘন সেমি
\(=\cfrac{1}{3}\times \cfrac{22}{7}[225\times 36 -25\times 12]\) ঘন সেমি
\(=\cfrac{1}{3}\times \cfrac{22}{7}[8100 -300]\) ঘন সেমি
\(=\cfrac{22\times \cancel{7800}2600}{\cancel3\times 7}\) ঘন সেমি
\(=\cfrac{57200}{7}\) ঘন সেমি
\(=8171\frac{3}{7}\) ঘন সেমি [Answer]