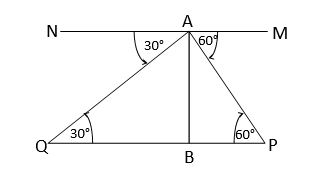
---

ধরি,উড়োজাহাজটির অবস্থান যখন \(A\) বিন্দুতে ছিল তখন পরপর দুটি কিলোমিটার ফলক \(P\) এবং \(Q\) এর অবনতি কোন যথাক্রমে \(60°\) এবং \(30°\) ছিল। এবং উড়োজাহাজটি \(AB\) মিটার উচ্চতায় উড়ছিল।

ধরি, \(MN||PQ\) এবং \( A,MN \) এর অপর অবস্থিত
\(∴ ∠MAP=60°\) এবং \(∠NAQ=30°\)
\(∠APB=\) একান্তর \(∠MAP=60° \)
এবং \(∠AQB=\) একান্তর \(∠NAQ=30° [∵MN||PQ]\)

সমকোণী ত্রিভূজ \(APB\) থেকে পাই
\(tan60°=\)লম্ব /ভূমি \(=\cfrac{AB}{PB} \)
বা, \(tan60°=\cfrac{AB}{PB} \)
বা, \(√3=\cfrac{AB}{PB} \)
বা, \(PB=\cfrac{AB}{√3}----(i) \)

সমকোণী ত্রিভূজ \(ABQ\) থেকে পাই
\(tan30°=\)লম্ব /ভূমি \(=\cfrac{AB}{BQ} \)
বা, \(tan30°=\cfrac{AB}{BQ} \)
বা, \(\cfrac{1}{√3}=\cfrac{AB}{BQ} \)
বা, \(BQ=AB√3----(ii)\)

\(∴PQ=1\) কিলোমিটার \(=1000 \)মিটার
\(PQ=PB+BQ \)
বা, \(1000=\cfrac{AB}{√3}+AB√3\) [\((i)\) এবং \((ii) \) থেকে]
বা, \(AB(\cfrac{1}{√3}+√3)=1000 \)
বা, \(\cfrac{AB(1+3)}{√3}=1000 \)
বা, \(AB=\cfrac{1000×√3}{4}=250√3\)

∴প্রথম ক্ষেত্রে যখন ফলক দুটি বিপরীত পাশে অবস্থিত, তখন উড়োজাহাজটির উচ্চতা \(250√3\) মিটার।