মাঠের মাঝখানে দাঁড়িয়ে মােহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে 30° উন্নতি কোণে এবং 2 মিনিট পরে দক্ষিণদিকে 60° উন্নতি কোণে দেখতে পেল। পাখিটি যদি একই সরলরেখা বরাবর 50√3 মিটার উঁচুতে উড়ে থাকে, তবে তার গতিবেগ কিলোমিটার প্রতি ঘন্টায় নির্ণয় করি।
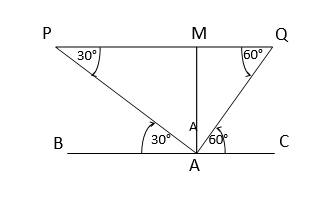
ধরি,মোহিত BC মাঠের A বিন্দুতে দাঁড়িয়ে পাখিটিকে প্রথমে P বিন্দুতে এবং 2 মিনিট পরে Q বিন্দুতে দেখে। যেহেতু পাখিটি একই উচ্চতায় উড়ছিল,তাই PQ||BC ও A বিন্দু থেকে পাখিটির উচ্চতা AM=50√3 মিটার
এখন,∠APM=একান্তর ∠BAP=30°
এবং ∠AQM=একান্তর ∠QAC=60° [∵PQ||BC]
সমকোণী ত্রিভূজ APM থেকে পাই
\( \tan30°=\cfrac{AM}{PM}=\cfrac{50√3}{PM}\)
বা, \(\cfrac{1}{√3}=\cfrac{50√3}{PM}\)
বা, \(PM=150 \)
সমকোণী ত্রিভূজ AMQ থেকে পাই
\(\tan60°=\cfrac{AM}{MQ}\)
বা, \(√3=\cfrac{50√3}{MQ}\)
বা, \(MQ=\cfrac{50√3}{√3}\)
বা, \(MQ=50\)
\(∴ PQ=PM+MQ=150+50=200\)
∴পাখিটি 2 মিনিটে যায় 200 মিটার ।
∴পাখিটির গতিবেগ ঘন্টায় \(=\cfrac{200×60}{2}\) মিটার
\(=6000\) মিটার \(=6\) কিলোমিটার ।