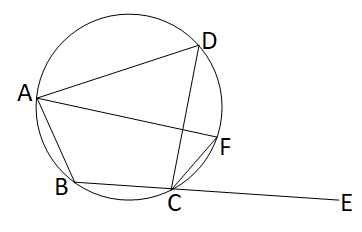
---

বৃত্তস্থ ABCD চতুর্ভূজের BC বাহুকে E পর্যন্ত বর্ধিত করা হল। \(\angle\)BAD এর সমদ্বিখন্ডক বৃত্তকে F বিন্দুতে ছেদ করে। CF যুক্ত করা হল।
প্রমান করতে হবে যে, CF,\(\angle\)DCE এর সমদ্বিখন্ডক।

প্রমানঃ \(\angle\)DAF=\(\angle\)DCF [একই বৃত্তাংশস্থ কোণ]
আবার,AF,\(\angle\)BAD এর সমদ্বিখন্ডক
∴\(\angle\)DAF=\(\frac{1}{2}\)\(\angle\)BAD
অর্থাৎ,\(\angle\)DCF=\(\frac{1}{2}\)\(\angle\)BAD----(i)

আবার,ABCD বৃত্তস্থ চতুর্ভূজের
\(\angle\)BAD+\(\angle\)BCD=2 সমকোণ [ বিপরীত কোণ]

আবার,BC সরলরেখার ওপর C বিন্দুতে CD দন্ডায়মান
∴\(\angle\)BCD+\(\angle\)DCE=2 সমকোণ
∴\(\angle\)BAD+\(\angle\)BCD=\(\angle\)BCD+\(\angle\)DCE
অর্থাৎ,\(\angle\)BAD= \(\angle\)DCE

(i)নং সমীকরনে \(\angle\)BAD= \(\angle\)DCE বসিয়ে পাই
\(\angle\)DCF=\(\frac{1}{2}\)\(\angle\)BAD=\(\frac{1}{2}\)\(\angle\)DCE

∴CF,\(\angle\)DCE এর সমদ্বিখন্ডক