একটি পার্কের একপ্রান্তে অবস্থিত 15 মিটার উঁচু একটি বাড়ির ছাদ থেকে পার্কের অপরপারে অবস্থিত একটি ইটভাটার চিমনির পাদদেশ ও অগ্রভাগ যথাক্রমে 30° অবনতি কোণ ও 60° উন্নতি কোণে দেখা যায়। ইটভাটার চিমনির উচ্চতা এবং ইটভাটা ও বাড়ির মধ্যে দূরত্ব নির্ণয় করি।
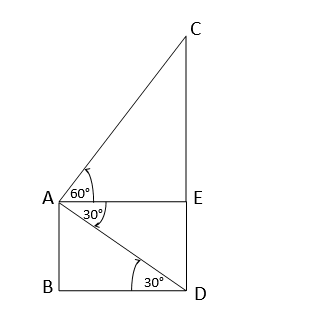
ধরি,AB একটি 15 মিটার উঁচু বাড়ি এবং CD ইটভাটার চিমনি। বাড়ির ছাদ A থেকে চিমনির পাদদেশ D এর অবনতি কোণ এবং অগ্রভাগ C এর উন্নতি কোণ যথাক্রমে 30° এবং 60°
A বিন্দু থেকে BD এর সমান্তরাল সরলরেখা CD কে E বিন্দুতে ছেদ করে ।
যেহেতু AE||BD
∴∠ADB=একান্তর ∠EAD=30°
সমকোণী ত্রিভূজ ABD থেকে পাই
tan30°=\(\cfrac{AB}{BD}=\cfrac{15}{BD}\)
বা,\(\cfrac{1}{√3}=\cfrac{15}{BD}\)
বা, \(BD=15√3 \)
আবার,AE=BD=15√3
সমকোণী ত্রিভূজ AEC থেকে পাই tan60° \(=\cfrac{CE}{AE}=\cfrac{CE}{15√3}\)
বা, \(√3=\cfrac{CE}{15√3}\)
বা, \(CE=45\)
CD=CE+ED=CE+AB=45+15=60
∴চিমনির উচ্চতা CD=60 মিটার এবং ইটভাটা ও বাড়ির দূরত্ব BD=15√3 মিটার ।