O কেন্দ্রীয় একটি বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ করি যে,\(\angle\)AOD + \(\angle\)BOC = 2\(\angle\)BPC যদি \(\angle\)AOD ও \(\angle\)BOC পরস্পর সম্পূরক হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি পরস্পর লম্ব।
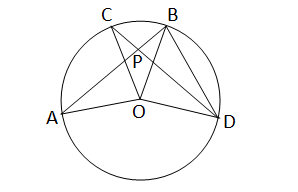
O কেন্দ্রীয় বৃত্তের AB এবং CD জ্যা পরস্পরকে P বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,\(\angle\)AOD+\(\angle\)BOC=2\(\angle\)BPC
অঙ্কনঃ B,D যুক্ত করা হল।
প্রমানঃ O কেন্দ্রীয় বৃত্তের AD চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)AOD এবং বৃত্তস্থ কোণ \(\angle\)ABD
∴\(\angle\)AOD=2\(\angle\)ABD
আবার,BC চাপের ওপর অবস্থিত কেন্দ্রস্থ কোণ \(\angle\)BOC এবং বৃত্তস্থ কোণ \(\angle\)BDC
∴\(\angle\) BOC=2\(\angle\)BDC
∴\(\angle\)AOD+\(\angle\)BOC=2\(\angle\)ABD+2\(\angle\)BDC
=2(\(\angle\)ABD+\(\angle\)BDC)=2(\(\angle\)PBD+\(\angle\)BDP)
আবার,∆BPD এর \(\angle\)BPC=\(\angle\)PBD+\(\angle\)BDP [∵বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টি]
∴\(\angle\)AOD+\(\angle\)BOC =2(\(\angle\)PBD+\(\angle\)BDP)=2\(\angle\)BPC (প্রমানিত)
যদি,\(\angle\)AOD+\(\angle\)BOC =2 সমকোণ হয় তবে,
2\(\angle\)BPC=\(\angle\)AOD+\(\angle\)BOC =2 সমকোণ
অর্থাৎ,\(\angle\)BPC=1 সমকোণ
∴AB ও CD পরস্পর লম্ব। (প্রমানিত)