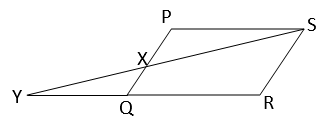
---

ধরি, \(PQRS\) একটি সামান্তরিক। \(S\) বিন্দুগামী একটি সরলরেখা \(PQ\) এবং বর্ধিত \(RQ\) কে যথাক্রমে \(X\) ও \(Y\) বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, \(PS:PX=QY:QX=RY:RS\)

প্রমানঃ \(∆PSX\) এবং \(∆QXY\) এর মধ্যে
\(∠PSX=∠XYQ\) [ \(∵PS∥YR \) এবং \(YS \) ছেদক]
\(∠SPX=∠XQY\) [ \(∵PS∥YR \) এবং \(PQ\) ছেদক]
এবং \(∠PXS=∠QXY\) (বিপ্রতীপ কোণ)
\(∴∆PSX\) এবং \(∆QXY\) সদৃশকোণী

অর্থাৎ, \(\cfrac{PX}{QX}=\cfrac{PS}{QY}=\cfrac{SX}{XY}\)
\(∴ \cfrac{PX}{QX}=\cfrac{PS}{QY}\)
বা, \(\cfrac{PS}{PX}=\cfrac{QY}{QX}----(i)\)

আবার \(∆SRY\) এবং \(∆QXY\) এর মধ্যে
\(∠SRY=∠XQY\)[ \(∵SR∥XQ \)এবং \(SY\) ছেদক]
\(∠RSY=∠QXY\) [ \(∵SR∥XQ \)এবং \(RY\) ছেদক]
এবং \(∠SYR=∠XYQ\) [একই কোণ]
\(∴ ∆SRY\) এবং \(∆QXY\) সদৃশকোণী

অর্থাৎ, \(\cfrac{RY}{QY}=\cfrac{SY}{XY}=\cfrac{RS}{QX} \)
\(∴ \cfrac{RY}{QY}=\cfrac{RS}{QX} \)
বা, \(\cfrac{RY}{RS}=\cfrac{QY}{QX}----(ii)\)

\((i)\) এবং \( (ii)\) নং থেকে পাই,
\(\cfrac{PS}{PX}=\cfrac{QY}{QX}=\cfrac{RY}{RS}\)
অর্থাৎ, \(PS:PX=QY:QX=RY:RS \)(প্রমানিত)