দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্তদুটি A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করি যে, CD=2PQ.
Loading content...
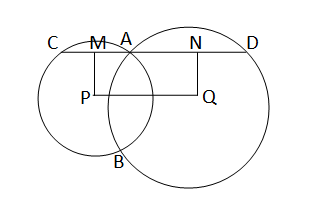
ধরি,P এবং Q কেন্দ্রীয় বৃত্তদুটি পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে। A বিন্দু দিয়ে PQ এর সমান্তরাল সরলরেখা P এবং Q কেন্দ্রীয় বৃত্তকে যথাক্রমে C এবং D বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,CD=2PQ
অঙ্কনঃ P এবং Q বিন্দু দিয়ে CD এর ওপর যথাক্রমে PM এবং QN লম্ব টানা হল।
প্রমানঃ যেহেতু PQ∥MN এবং PM⊥CD ও QC⊥CD,তাই PQNM একটি আয়তক্ষেত্র ।
∴PQ=MN
আবার,PM,CA কে সমদ্বিখন্ডিত করেছে।
∴MA=\(\frac{1}{2}\) CA
অনুরূপভাবে QN,AD কে সমদ্বিখন্ডিত করেছে।
∴AN=\(\frac{1}{2}\)AD
∴MN=MA+AN
=\(\frac{1}{2}\)CA+\(\frac{1}{2}\)AD
=\(\frac{1}{2}\)(CA+AD)
=\(\frac{1}{2}\) CD
বা,CD=2MN=2PQ [∵PQ=MN]
∴CD=2PQ (প্রমানিত)
