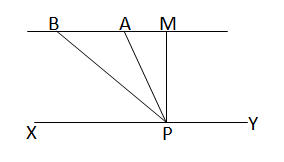
---

এক ব্যক্তি XY সমতলের কোনো একটি স্থান P বিন্দু থেকে একটি বিমানকে A বিন্দুতে \(\angle\)APX=60° উন্নতি কোণে দেখে। 15 সেকেন্ড পরে ঐ P বিন্দু থেকেই বিমানটিকে আবার B বিন্দুতে \(\angle\)BPX= 30° উন্নতি কোণে দেখে। ধরি, বিমানটি PM= 1500√3 মিটার উঁচুতে থেকে একই সরলরেখা MAB বরাবর উড়ে থাকে ।

\(\angle\)MAP=একান্তর \(\angle\)APX=60\(^o\)
\(\angle\)MBP=একান্তর \(\angle\)BPX=30\(^o\)

\(\triangle\)AMP থেকে পাই,
\(\cfrac{MP}{AM}=tan 60^o\)
বা, \(\cfrac{1500\sqrt3}{AM}=\sqrt3\)
বা, \(AM=\cfrac{1500\sqrt3}{\sqrt3}=1500\)

\(\triangle\)BMP থেকে পাই,
\(\cfrac{MP}{BM}=tan 30^o\)
বা, \(\cfrac{1500\sqrt3}{BM}=\cfrac{1}{\sqrt3}\)
বা, \(BM= 1500\sqrt3\times \sqrt3=4500\)

এখন, AB=BM-AM=4500-1500=3000

\(\therefore\) বিমানটি 15 সেকেন্ডে যায় 3000 মিটার
\(\therefore\) বিমানটির গতিবেগ \(=\cfrac{3000}{15}\) মিটার/সেকেন্ড \(=200\) মিটার/সেকেন্ড ।