Welcome to Ganitsarani

1. নিন্মলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচিত করো । \([1\times 6=6]\)

(i) একটি মেশিনের বর্তমান মূল্য 2P টাকা এবং প্রতিবছর মেশিনটির দাম 2r% হ্রাস হলে,2n বছর পরে মেশিনটির দাম হবে

(a) \(P\left(1-\cfrac{r}{100}\right)^n\) (b) \(2P\left(1-\cfrac{r}{50}\right)^n\) (c) \(P\left(1-\cfrac{r}{50}\right)^{2n}\) (d) \(2P\left(1-\cfrac{r}{50}\right)^{2n}\)

(ii) যদি \(p+q=\sqrt{13}\) এবং \(p-q\sqrt 5\) হয়, তবে pq এর মান হবে

(a) 2 (b) 18 (c) 9 (d) 8

(iii) O কেন্দ্রীয় বৃত্তের AB.একটি ব্যাস। P পরিধির উপরিস্থিত যে কোনো একটি বিন্দু। \(\angle\)POA = 120° হলে \(\angle\)PBO -এর পরিমাপ

(a) 30° (b) 60° (c) 90° (d) 120°

(iv) যদি, \(3x=5sin\theta\) এবং \(4y=5cos\theta\) হয়, তবে নীচের কোন সম্পর্কটি সঠিক ?

(a) \(\cfrac{9x^2}{25}+\cfrac{16y^2}{25}=1\) (b) \(\cfrac{9x^2}{25}+\cfrac{16y^2}{25}=0\) (c) \(\cfrac{9x^2}{25}-\cfrac{16y^2}{25}=1\) (d) \(\cfrac{16x^2}{25}+\cfrac{9y^2}{25}=1\)

(v) একটি লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ এবং উচ্চতা দ্বিগুণ করলে, শঙ্কুটির আয়তন বৃদ্ধি পায়

(a) \(300\%\) (b) \(400\%\) (c) \(700\%\) (d) \(800\%\)

(vi) উচ্চ সাজানো 8, 9, 12, 17, x+2, x+4, 30, 31, 34, 39 তথ্যের মধ্যমা 24 হলে, x-এর মান

(a) 22 (b) 21 (c) 20 (d) 24

2. শূন্যস্থান পূরণ করো । (যেকোনো পাঁচটি ) \([1\times 5=5]\)

(i) যে ব্যক্তি টাকা ধার দেন তাকে ----- বলে।
(ii) (x+2) এবং (x-3) এর মধ্য সমানুপাতী x হলে x এর মান ___ ।
(iii) দুটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ না করলে বৃত্ত দুটির সর্বাধিক সংখ্যায় _____ টি সাধারণ স্পর্শক অঙ্কন করা যায়।
(iv) \(\cfrac{3\pi}{8}\) কোণটির সম্পূরক কোণের বৃত্তীয় মান _____।
(v) একমুখ কাটা একটি পেনসিলের আকার শঙ্কু ও ___________সমন্বয়।
(vi) \(x_1, x_2, x_3, .......x_n\) এর গড় \(\bar{x}\) হলে, \(ax_1, ax_2, ax_3, ........ ax_n\) -এর গড় ________, যেখানে \(a≠0\)

3. সত্য বা মিথ্যা লেখো । (যেকোনো পাঁচটি ) \([1\times 5=5]\)

(i) নির্দিষ্ট পরিমান টাকার বার্ষিক নির্দিষ্ট শতকরা হার সুদে 1 বছরে চক্রবৃদ্ধি সুদের পরিমান এবং সরল সুদের পরিমান সমান।
(ii) \(x^2-x=k (2x-1) \)সমীকরণের বীজদ্বয়ের সমষ্টি শূন্য হলে k এর মান \(\cfrac{1}{2}\) ।
(iii) দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ।
(iv) যদি \(0°\lt \alpha\lt 90°\) হয় তাহলে \(sec^2 \alpha+cos^2\alpha\) এর সর্বনিম্ন মান 2
(v) দুটি ঘনকের আয়তনের অনুপাত 64:27 হলে তাদের সমগ্রতলের ক্ষেত্রফলের অনুপাত হবে 9:16।
(vi) 16, 15, 17, 16, 15, x, 19, 17, 14 তথ্যের সংখ্যাগুরু মান 15 হলে x এর মান হবে 15।

4. নিন্মলিখিত প্রশ্নগুলির উত্তর দাও । (যেকোনো দশটি ) \([2\times 10=20]\)

(i) বার্ষিক নির্দিষ্ট শতকরা চক্রবৃদ্ধি হার সুদে কিছু টাকা \(n\) বছরে দ্বিগুণ হলে, কত বছরে 4 গুণ হবে?
(ii) একটি ব্যবসায় সুজয় এবং পলাশের মূলধনের অনুপাত 4:5 এবং তাদের লাভের অনুপাত 2:3। যদি সুজয় 10 মাসের জন্য অর্থ বিনিয়োগ করে থাকে তবে পলাশ কত সময়ের জন্য অর্থ বিনিয়োগ করেছিল?
(iii) যদি \(\cfrac{x}{y}\propto x+y\) এবং \(\cfrac{y}{x}\propto x – y\) হয়, তবে দেখাও যে, \((x^2 –y^2)\) একটি ধ্রুবক রাশি।
(iv) \((b-c)x^2+(c-a)x+(a-b)=0\) দ্বিঘাত সমীকরণের বীজদ্বয় সমান হলে। প্রমাণ করাে \(2b = a+c\)
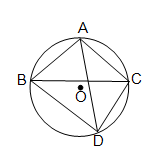
(v)

পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB = AC; \(\angle\)ABC = 32° হলে , \(\angle\)BDC-এর মান নির্ণয় করি।

(vi) পাশের চিত্রে DE||BC, BE||XC, এবং \(\cfrac{AD}{DB}=\cfrac{2}{1}\)হলে \(\cfrac{AX}{XB}\)এর মান নির্ণয় করো।
(vii)

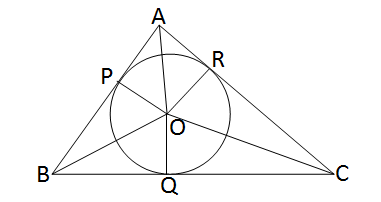
পাশের চিত্রে ABC ত্রিভূজটি একটি বৃত্তে পরিলিখিত এবং বৃত্তকে P,Q,R বিন্দুতে স্পর্শ করে। যদি AP=4 সেমি,BP=6 সেমি,AC=12 সেমি এবং BC=x সেমি হয়,তবে x এর মান নির্ণয় করি।

(viii) যদি \(sin\theta +cosec\theta=2\) হয়, তবে \((sin^{10}\theta+cosec^{10}\theta)\) এর মান নির্ণয় করো।
(ix) যদি \( tan4\theta . tan6\theta =1\) এবং \(6\theta\) একটি ধনাত্মক সূক্ষ্মকোণ হয়, তবে \(tan5\theta\) এর মান নির্ণয় করো।
(x) একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য, প্রস্থ এবং উচ্চতা যথাক্রমে a, b এবং c একক এবং a+b+c = 25, ab+bc+ca = 240.5 হলে, ঘরের মধ্যে যে বৃহত্তম দৈর্ঘ্যের দণ্ডটি রাখা যাবে তার দৈর্ঘ্য কত হবে হিসাব করে লিখি।।
(xi) একটি লম্ব বৃত্তাকার চোঙের পার্শ্বতলের ক্ষেত্রফল c বর্গএকক, ভূমির ব্যাসার্ধের দৈর্ঘ্য\(r\) একক এবং আয়তন V ঘনএকক হলে \(\cfrac{cr}{V}\)এর মান নির্ণয় করো।
(xii) যদি \(u_i =\cfrac{x_i-25}{10} ,\sum f_i u_i=20\) এবং \(\sum f_i=100\) হয়, তাহলে \(\bar{x}\)-এর মান নির্ণয় কর ।

5. যেকোনো একটি প্রশ্নের উত্তর দাও \([1 \times 5=5] \)

(i) রমেনবাবু মােট 3.70,000 টাকা তিনটি ব্যাঙ্কে জমা রাখেন। তিনটি ব্যাঙ্কের বার্ষিক সরল সুদের হার যথাক্রমে 4%, 5% এবং 6%, 1 বছর পর তাঁর তিনটি ব্যাঙ্কে মােট সুদের পরিমাণ সমান হয়। তিনি তিনটি ব্যাঙ্কে কত টাকা করে জমা রেখেছিলেন?
(ii) বছরের শুরুতে শ্রীকান্ত ও সৈফুদ্দিন। 2.40.000 টাকা ও 3.00,000 টাকা দিয়ে একটি মিনিবাস ক্রয় করে চালাতে থাকেন। চার মাস পর তাদের বন্ধু পিটার 81,000 টাকা নিয়ে তাদের সঙ্গে যােগ দিলে শ্রীকান্ত ও সৈফুদ্দিন তাদের মূলধনের অনুপাতে সেই টাকা তুলে নেন। বছরের শেষে 39150 টাকা লাভ হলে, লভ্যাংশ থেকে কে কত টাকা পাবেন?

6. যেকোনো একটি সমাধান করো । \([1 \times 3=3] \)

(i) সমাধান করো: \(\cfrac{x-3}{x+3}-\cfrac{x+3}{x-3}+6\cfrac{6}{7}=0\) \((x\ne-3,3)\)
(ii) কলমের মূল্য প্রতি ডজনে 6 টাকা কমলে 30 টাকায় আরো 3টি বেশি কলম পাওয়া যাবে। কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করো।

7. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) যদি \(x=2, y=3\) এবং \(z=6\) হয়, তবে,
\(\cfrac{3√x}{√y+√z}-\cfrac{4√y}{√z+√x}+\cfrac{√z}{√x+√y}\) -এর মান হিসাব করে লিখি ।
(ii) একটি হোস্টেলের ব্যয় আংশিক ধ্রুবক ও আংশিক ওই হোস্টেলবাসী লোকসংখ্যার সঙ্গে আছে। লোকসংখ্যা 120 হলে ব্যয় 2000 টাকা হয় এবং লোকসংখ্যা 100 হলে ব্যয় 1700 টাকা হয়। ব্যয় 1,880 টাকা হলে লোকসংখ্যা কত হবে?

8. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) যদি \(\cfrac{b}{a+b}=\cfrac{a+c-b}{b+c-a}=\cfrac{a+b+c}{2a+b+2c}\) হয়, (যেখানে \(a+b+c \ne0\)) তবে দেখাও যে, \(\cfrac{a}{2}=\cfrac{b}{3}=\cfrac{c}{4}\)
(ii) \(x= \cfrac{8ab}{a+b}\) হলে \(\cfrac{x+4a}{x-4a}+\cfrac{x+4b}{x-4b}\)=কত?

9. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) প্রমাণ করো যে, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।
(ii) পিথাগোরাসের উপপাদ্যটি বিবৃতি করো ও প্রমাণ করো।

10. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) O কেন্দ্রীয় বৃত্তের AB একটি ব্যাস। বৃত্তের উপরিস্থ P বিন্দু থেকে AB ব্যাসের ওপর একটি লম্ব অঙ্কন করা হয় যা AB-কে N বিন্দুতে ছেদ করে। প্রমাণ করো, PB\(^2\) = AB.BN
(ii) যুক্তি দিয়ে প্রমাণ করো যে,কোনো বৃত্তের দুটি সমান দৈর্ঘ্যের জ্যা কেন্দ্র থেকে সমদূরবর্তী।

11. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করো যার ভূমির দৈর্ঘ্য 7.8 সেমি এবং সমান বাহু দুটির প্রত্যেকটির দৈর্ঘ্য 6.5 সেমি। ওই ত্রিভুজের একটি অন্তবৃত্ত অঙ্কন করো।
(ii) জ্যামিতিক উপায়ে √21-এর মান নির্ণয় করো।

12. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 3=6] \)

(i) প্রমাণ করো যে,\(\cfrac{sec\theta+tan\theta-1}{tan\theta-sec\theta+1}=\cfrac{1+sin\theta}{cos\theta}\)
(ii) মান নির্ণয় করো : \(\cfrac{tan60^\circ-tan30^\circ}{1+tan60^\circ tan30^\circ}+cos60^\circ cos30^\circ+sin60^\circ sin30^\circ\)
(iii) প্রমাণ করো যে \(cosec^222° cot^2 68°\) \(=sin^222°+sin^268°+cot^268°\)

13. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) একটি পার্কের এক প্রান্তে অবস্থিত 15 মিটার উঁচু একটি বাড়ির ছাদ থেকে পার্কের অপর প্রান্তে অবস্থিত একটি ইটভাটার চিমনি পাদদেশ ও অগ্রভাগ যথাক্রমে 30° অবনতি কোণ ও 60° উন্নতি কোণে দেখা যায়। ইটভাটার চিমনির উচ্চতা এবং ইটভাটা ও বাড়ির মধ্যে দূরত্ব নির্ণয় করো।
(ii) একটি পাখি ভূমিতলের সঙ্গে সমান্তরাল রেখায় 200 মিটার উঁচু দিয়ে উত্তর থেকে দক্ষিণ দিকে যাচ্ছিল। মাঠের মাঝখানে দাঁড়িয়ে সুশোভন প্রথমে পাখিটিকে উত্তরদিকে 30° কোণে দেখতে পেল। 3 মিনিট পরে আবার দক্ষিণ দিকে 45° কোণে দেখতে পেল। আসন্ন পূর্ণসংখ্যায় কিলোমিটারে পাখিটির গতিবেগ ঘণ্টায় কত ছিল নির্ণয় করো। [√3=1.732 (প্রায়)]

14. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 4=8] \)

(i) গ্রামের আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 20 মিটার এবং 15 মিটার। ওই মাঠের ভিতরে চারটি কোণে পিলার বসানাের জন্য 4 মিটার দৈর্ঘ্যবিশিষ্ট চারটি ঘনকাকৃতি গর্ত কেটে অপসারিত মাটি অবশিষ্ট জমির উপর ছড়িয়ে দেওয়া হলাে। মাঠের তলের উচ্চতা কতটা বৃদ্ধি পাবে তা নির্ণয় করাে।
(ii) 1 সেমি. পুরু সিসার পাতের তৈরি একটি ফাঁপা গোলকের বাহিরের ব্যাসার্ধের দৈর্ঘ্য 6 সেমি.। গোলকটি গলিয়ে 2 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি নিরেট লম্ব বৃত্তাকার দণ্ড তৈরি করা হলে, দণ্ডটির দৈর্ঘ্য কত হবে হিসাব করে লিখি।
(iii) লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবুর ভূমিতলের ক্ষেত্রফল 13.86 বর্গমিটার। তাঁবুটি তৈরি করতে 5775 টাকা মূল্যের একটি ত্রিপল লাগে এবং । বর্গমিটার ত্রিপলের মূল্য 150 টাকা হলে তাবুটির উচ্চতা নির্ণয় করো। তাঁবুটিতে কত লিটার বায়ু আছে?

15. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 4=8] \)

(i) যদি নীচের পরিসংখ্যা বিভাজন তালিকার নম্বরের যৌগিক গড় 24 হয়, তবে p-এর মান নির্ণয় করি।

নম্বর	0-10	10-20	20-30	30-40	40-50
ছাত্রসংখ্যা	15	20	35	p	10

(ii) নীচের পরিসংখ্যা বিভাজনের ওজাইভ অঙ্কন করি এবং সেই ওজাইভ থেকে মধ্যমা নির্ণয় করি।

শ্রেণি	0-10	10-20	20-30	30-40	40-50	50-60
পরিসংখ্যা	7	10	23	50	6	4

(iii) নীচের প্রদত্ত ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি থেকে পরিসংখ্যা বিভাজন ছক তৈরি করে তথ্যটির সংখ্যাগুরুমান নির্ণয় করো :

শ্রেণি সীমানা	10 এর কম	20 এর কম	30 এর কম	40 এর কম	50 এর কম	60 এর কম	70 এর কম	80 এর কম
পরিসংখ্যা	4	16	40	76	96	112	120	125