Welcome to Ganitsarani

1. নিন্মলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচিত করো । \([1\times 6=6]\)

(i) এক ব্যক্তি একটি ব্যাঙ্কে 100 টাকা জমা রেখে, 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা। বার্ষিক চক্রবৃদ্ধি সুদের হার

(a) 10% (b) 20% (c) 5% (d) \(120\cfrac{1}{2}\)%

(ii) \(ax^2+bx+c=0 (a≠0) \) সমীকরণের বীজদ্বয় সমান হলে

(a) \(c =-\cfrac{b}{2a}\) (b) \(c =\cfrac{b}{2a}\) (c) \(c =-\cfrac{b^2}{4a}\) (d) \(c =\cfrac{b^2}{4a}\)

(iii) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। \(\angle\)AOB=60° হলে \(\angle\)COD = কত?

(a) 30° (b) 40° (c) 120° (d) 60°

(iv) \( 2 cos3\theta=1 \)হলে, \(\theta\)-এর মান

(a) 10° (b) 15° (c) 20° (d) 30°

(v) দুটি ঘনকের আয়তনের অনুপাত 1:27 হলে, ঘন দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত হবে

(a) 1:3 (b) 1:8 (c) 1:9 (d) 1:18

(vi) 8,15,10,11 ,7,9,11,13,16 -এর মধ্যমা

(a) 15 (b) 10 (c) 11.5 (d) 11

2. শূন্যস্থান পূরণ করো । (যেকোনো পাঁচটি ) \([1\times 5=5]\)

(i) একটি ব্যবসায় রাজু ও আসিফের মূলধনের অনুপাত 5:4 এবং রাজু মোট লাভের ৪০ টাকা পেলে আসিফ পায় ------টাকা।
(ii) \(x \propto y\) এবং \(x \propto z\) হলে, \((y+z) \propto\)----
(iii) একই চাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ -----
(iv) যদি \(sin c=\cfrac{4}{5}\) হয়, তবে \(cos c\times cosec c= -----\)
(v) একটি লম্ব বৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হলে,চোঙটির ব্যাসের দৈর্ঘ্য – একক।
(vi) যৌগিক গড়, মধ্যমা, সংখ্যাগুরুমান হলো _____ প্রবণতার মাপক ।

3. সত্য বা মিথ্যা লেখো । (যেকোনো পাঁচটি ) \([1\times 5=5]\)

(i) \( 100\) টাকায় বার্ষিক \(r \%\) হারে \(n\) বছরে মোট সুদের পরিমাণ হলো \(rn\) ।
(ii) \(ab:c^2 , bc:a^2\) এবং \(ca:b^2\) -এর যৌগিক অনুপাত 1:1
(iii) বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি সর্বদা পরস্পর পূরক।
(iv) \( tanA tanB=1\) হলে \(A+B=90°\) হয়।
(v) দুটি সদৃশ্য ত্রিভুজের বাহুগুলির দৈর্ঘ্য সর্বদা সমান হয়।
(vi) একটি পরিসংখ্যা বিভাজনের মধ্যমা যে লেখচিত্রের সাহায্যে পাওয়া যায় তা হল ওজাইভ।

4. নিন্মলিখিত প্রশ্নগুলির উত্তর দাও । (যেকোনো দশটি ) \([2\times 10=20]\)

(i) 400 টাকার 2 বছরে সমূল চক্রবৃদ্ধি 441 টাকা হলে, বার্ষিক শতকরা চক্রবৃদ্ধি সুদের হার কত?
(ii) একটি অংশীদারি ব্যবসায় তিনজনের মূলধনের অনুপাত 3:8:5 এবং প্রথম ব্যক্তির লাভ তৃতীয় ব্যক্তির লাভের থেকে 60 টাকা কম হলে, ব্যবসায় মোট কত লাভ হয়েছিল?
(iii) \((√15+√3)\) এবং \((√10+√8)\) এর মধ্যে কোনটি বড় ?
(iv) \(x∝y, y∝z\)এবং \(z∝x\) হলে, অশূন্য ভেদ ধ্রুবক তিনটির গুণফল নির্ণয় করাে।
(v) ABCD আয়তাকার চিত্রের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে OB=6 সেমি, OD=8 সেমি এবং OA=5 সেমি। OC-এর দৈর্ঘ্য নির্ণয় করো।
(vi) একটি বৃত্তে দুটি জ্যা AB এবং AC পরস্পর লম্ব। AB=4 সেমি ও AC=3 সেমি হলে বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।
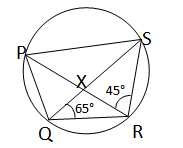
(vii)

পাশের ছবির PQRS বৃত্তস্থ চতুর্ভুজের কর্ণদ্বয় পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করেছে যে ∠PRS = 65° এবং ∠RQS = 45°; ∠SQP ও ∠RSP-এর মান হিসাব করে লিখি।

(viii) (tan 1°× tan2° × tan3°.................. tan89°) -এর মান নির্ণয় করি।
(ix) \(sin^6⁡α+cos^6⁡α+3sin^2⁡ α.cos^2⁡α \)এর মান নির্ণয় করো।
(x) দুটি লম্ববৃত্তাকার চোঙের উচ্চতার অনুপাত 1:2 এবং ভূমির পরিধির অনুপাত 3:4 হলে, তাদের আয়তনের অনুপাত কত?
(xi) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি এবং আয়তন 100π ঘনসেমি হলে, শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য কত হবে?
(xii) \(u_i=\cfrac{x_i-25}{10},∑f_i u_i=20,∑f_i=100\) তাহলে \(\bar{x}\) এর মান নির্ণয় করো।

5. যেকোনো একটি প্রশ্নের উত্তর দাও \([1 \times 5=5] \)

(i) কোনো মূলধনের 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদ যথাক্রমে 8,400 টাকা ও 8,652 টাকা হলে মূলধন ও বার্ষিক সরল সুদের হার নির্ণয় করো।
(ii) তিনবন্ধু যথাক্রমে 8,000 টাকা, 10,000 টাকা ও 12,000 টাকা সংগ্রহ করে এবং ব্যাঙ্ক থেকে কিছু টাকা ঋণ নিয়ে একটি ব্যবসা শুরু করেন। বছরের শেষে তারা দেখলেন 13,400 টাকা লাভ হয়েছে। সেই লাভ থেকে ব্যাঙ্কের বছরের কিস্তি 5,000 টাকা শোধ দেওয়ার পর বাকি টাকা তারা মূলধনের অনুপাতে ভাগ করে নিলেন। লভ্যাংশ থেকে কে কতো টাকা পাবেন ?

6. যেকোনো একটি সমাধান করো । \([1 \times 3=3] \)

(i) সমাধান করো :
\(\cfrac{1}{(x-1)(x-2)}\) \(+\cfrac{1}{(x-2)(x-3)} \) \(+\cfrac{1}{(x-3)(x-4)}\) \(=\cfrac{1}{6} ,\) \( x≠1,2,3,4\)
(ii) \(ax^2+bx+c=0 (a≠0)\) সমীকরণের একটি বীজ অপরটির দ্বিগুণ হলে, দেখাও যে, \(2b^2=9ac\)

7. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) \(\cfrac{√5}{√3+√2}-\cfrac{3√3}{√2+√5}+\cfrac{2√2}{√3+√5}\) সরল করো
(ii) \(a^2+b^2∝ab\) হলে, প্রমাণ করি যে, \(a+b ∝ a-b\).

8. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) যদি \(\cfrac{ay−bx}{c}=\cfrac{cx−az}{b}=\cfrac{bz−cy}{a}\) হয়, তবে প্রমাণ করো \(\cfrac{x}{a}=\cfrac{y}{b}=\cfrac{z}{c}\)
(ii) \(x^2:(by+cz)=y^2:(cz+ax)=z^2:\) \((ax+by)=1\) হলে দেখাও যে, \(\cfrac{a}{a+x}+\cfrac{b}{b+y}\) \(+\cfrac{c}{c+z}=1\)

9. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) প্রমাণ করো যে কোনো বৃত্তের একটি বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্ৰস্থ কোন ঐ চাপের দ্বারা গঠিত যে কোন বৃত্তস্থ কোণের দ্বিগুণ।
(ii) প্রমাণ করো যে, কোনো সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।

10. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 3=3] \)

(i) O কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD হলে, প্রমাণ করো যে, AB+CD=BC+DA
(ii) ABC ত্রিভুজের \(\angle\)A সমকোণ। CD মধ্যমা হলে, প্রমাণ করো যে, BC\(^2\)=CD\(^2\)+3AD\(^2\)

11. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) একটি সমকোণী ত্রিভুজ অঙ্কন করো যার সমকোণ সংলগ্ন বাহুদুটির দৈর্ঘ্য 4 সেমি. ও ৪ সেমি.। ত্রিভুজটির পরিবৃত্ত অঙ্কন করো। (কেবলমাত্র অঙ্কনচিহ্ন দিতে হবে।)
(ii) একটি ত্রিভুজ অঙ্কন করো যার তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 7 সেমি, 6 সেমি এবং 5.5 সেমি। ঐ ত্রিভুজটির একটি অন্তবৃত্ত অঙ্কন করো।

12. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 3=6] \)

(i) \( sin\theta + sin^2\theta=1 \)হলে, প্রমাণ করো \(cos^2\theta+cos ^4\theta=1 \)
(ii) \(sin17^ \circ =\cfrac{x}{y}\) হলে, তবে দেখাও যে, \(sec17^\circ-sin73^\circ=\cfrac{x^2}{y\sqrt{y^2-x^2}}\)
(iii) \(cosec\theta+cot\theta=3 \) হলে, \(cosec\theta\) ও \(cot\theta\) উভয়ের মান নির্ণয় করো।

13. যেকোনো একটি প্রশ্নের উত্তর দাও । \([1 \times 5=5] \)

(i) একটি তিনতলা বাড়ির ছাদে 3.3 মিটার দৈর্ঘ্যের একটি পতাকা আছে। রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয়। বাড়িটির উচ্চতা নির্ণয় করো। [tan 50 ° = 1.192]
(ii) একটি উড়ো জাহাজ থেকে রাস্তায় পরপর দুটি কিলোমিটার ফলকের অবনতি কোণ যথাক্রমে 60° ও 30° হলে, উড়ো জাহাজটির উচ্চতা নির্ণয় করো, (i) যখন ফলক দুটি উড়ো জাহাজের বিপরীত পাশে অবস্থিত, (ii) যখন ফলক দুটি উড়ো জাহাজের একই পাশে অবস্থিত।

14. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 4=8] \)

(i) একটি লম্ববৃত্তাকার চোঙের উচ্চতা উহার ব্যাসার্ধের দ্বিগুণ। যদি 6 গুণ হতো তবে চোঙটির আয়তন 539 ঘনডেসিমি বেশি হতো। চোঙটির উচ্চতা কত?
(ii) সমান ভূমিতলের ব্যাস এবং সমান উচ্চতাবিশিষ্ট একটি নিরেট শঙ্কু, একটি নিরেট অর্ধগোলক এবং একটি নিরেট চোঙের আয়তনের অনুপাত নির্ণয় করি।
(iii) 2.1 মিটার দীর্ঘ, 1.5 মিটার প্রশস্ত একটি আয়তঘনাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ঐ চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা কতটা বৃদ্ধি পাবে নির্ণয় করো।

15. যেকোনো দুটি প্রশ্নের উত্তর দাও । \([2 \times 4=8] \)

(i) যদি নীচের পরিসংখ্যা বিভাজন তালিকার নম্বরের যৌগিক গড় 24 হয়, তবে p-এর মান নির্ণয় করি।

শ্রেণি-সীমানা(নম্বর)	0-10	10-20	20-30	30-40	40-50
ছাত্রসংখ্যা	15	20	35	p	10

(ii) নীচের পরিসংখ্যা বিভাজনের ক্ষুদ্রতর সূচক ওজাইভ অঙ্কন করো।

গাছের পাতার দৈর্ঘ্য	120-130	130-140	140-150	150-160	160-170	170-180	180-190
পাতার সংখ্যা	4	6	10	14	6	6	4

(iii) নীচের পরিসংখ্যা বিভাজনের সংখ্যাগুরু মান নির্ণয় করো :

শ্রেণি সীমা	45-54	55-64	65-74	75-84	85-94	95-104
পরিসংখ্যা	8	13	19	32	12	6